
This article explains the difference between linear and exponential series and shows how to model them using Excel.
Rabbit population growth is a good example of an exponential progression and in this lesson you’ll forecast the growth in a rabbit population for each month in a four-year period. You may be surprised how quickly they can multiply.
This article is an unedited lesson from one of the 25 short focused lessons Session 2 of my “Essential Skills” book.
Leave me a comment if you find the lesson useful.
- Excel 365
- Excel 2021
- Excel 2019
- Excel 2016
- February 12, 2022
- No Comments
note
Linear and exponential series can also be defined using the Ribbon
Here’s how you could have used the Ribbon to complete this lesson:
- Enter the value 200 into cell B4.
- Select cells B4:B51.
- Click: Home->Editing->
Fill->Series…
The Series dialog appears.
- Enter the following values into the Series dialog:
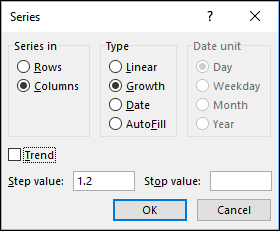
Note that the value: 1.2 is used because an exponential (growth) series multiplies each start value by the step value.
important
A synonym is a word you use when you can’t spell the other one.
Baltasar Gracián
(Philsopher 1601-1658)
Excel uses different terminology in various menus, dialog boxes and task panes that mean the same thing (in the context of this lesson):
Series, Forecast and Trend mean the same thing.
Growth and Exponential also mean the same thing.
In this lesson I’ll consistently use the terminology Series and Exponential.
note
Excel can calculate a linear series when the step values of cells are not equal
Excel calculates a linear series (AutoFill also calls this a fill series) using this formula:
Start Value + Step Value
Sometimes you may need to produce linear series values from a series of numbers that have different step values. For example, consider this range:

In this case Excel will use a more complex mathematical operation (called the least-squares algorithm) to determine the correct step value to use. In the above example, Excel would calculate a step value of 1.01.
trivia
According to an old legend, the inventor of the game of Chess presented his new game to a powerful king. The king was so pleased with the game that he offered the inventor any reasonable reward.
The inventor asked for one grain of rice for the first square on the chessboard, two for the second, four for the third… and so on for each of the 64 squares on the chessboard.
The king thought the inventor was foolish to ask for such a simple gift. Much later he found that there was not enough rice in the entire world to fulfil the inventor’s request.
With the Excel skills you have learned in this lesson, you should easily be able to model the King’s dilemma and discover exactly how many grains of rice would have been needed (about 18.5 Quintillion).
Lesson 2-18: Understand linear and exponential series
Linear series
In: Lesson 2‑14: Use AutoFill for text and numeric series, you used AutoFill’s Fill Series method to automatically create these numeric series.
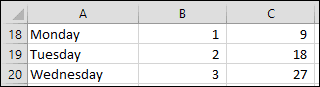
These are both examples of Linear series.
To create the linear series in column C you selected cells C18:C19 before AutoFilling down the column:
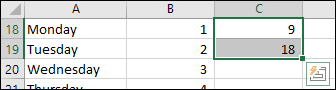
To calculate a linear series Excel first identifies the step value. The linear series in column C has a step value of nine (18-9=9).
When you use AutoFill’s Fill Series method, Excel adds the step value to the start value (the number shown in the previous cell).
In the above example, if you AutoFill down to cell C20, the value shown in cell C20 will be 27. This is calculated by adding the step value of 9 to the start value of 18.
This is an example of a very simple linear series. Excel is also able to calculate a linear series even when the step values of the selected cells are not equal (see sidebar).
Exponential (or Growth) series
An exponential series is calculated by multiplying (rather than adding) the start value by the step value. This type of series is usually referred to as an exponential (rather than linear) series. Excel also uses the term growth series as a synonym for exponential series (see sidebar).
Here’s an example:
- A truly excellent restaurant opens in town. On the first day they only have one customer, but the customer is so delighted by the food, service and value that the customer tells two friends.
- The next day the two friends eat there, and the restaurant has two diners.
- The two friends are also so pleased with their experience that they each tell two friends. On the third day the restaurant has four diners.
You can see that the restaurant owner might expect that this trend will continue and that each day the number of diners will double (in Excel’s terminology, the step value is 2). Eventually, of course, the restaurant will become full and the trend will have to end (in Excel’s terminology the number of seats in the restaurant is the stop value).
In this lesson you will model this type of exponential series.
1. Open the sample file Rabbit Population in Excel.
2. If the rabbit population of an island increases at the rate of 20% per month, use an exponential progression to calculate how a newly introduced community of 200 rabbits will grow in four years.
- Type the value: 200 into cell B4 to set the rabbit population at the beginning of the period.
- Type the value: 240 into cell B5 to set the rabbit population after one month.
- Select the range B4:B5.
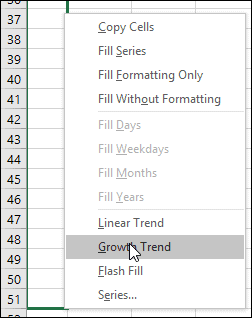
- Hold down the right mouse button on the AutoFill handle at the bottom-right of the selected range and drag down to AutoFill to cell B51.
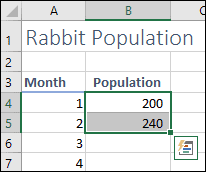
- Click Growth Trend from the shortcut menu. Note that this is the shortcut menu’s synonym for: Exponential Series.
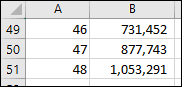
After four years (48 months) the 200 rabbits will have grown to a population of a little over a million.
3. Save your work as Rabbit Population-1.
Here’s the sample file at the end of the session. If you ran into any problems you can study the finished workbook to identify the problem.
I hope that you enjoyed the lesson and now have a complete understanding of Linear and Exponential series.

This lesson is excerpted from the above book. Smart Method books are the only up-to-date Excel books published with regular new editions published whenever significant new features are added to Excel.
Available as both a paper printed book and as an e-book you can instantly download today.
Some of the things you will learn





Related Articles
Keyboard shortcut for autofill in Excel
This article explains several different ways to carry out an AutoFill using the keyboard in Excel and explains Flash Fill and the Repeat command.



